If we take the rectangle generated by the Vesica Pisces in the diagram on the previous page, and turn it on its side we end up with the following:-

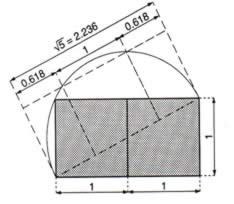
You can see that if you divide this rectangle into two equal squares, and then move one of those squares into the centre of the rectangle, who's base is created by the diagonal, you are left with two smaller Golden Mean rectangles who's shortest side is proportionally 0.618 in relation to the original.

It is therefore shown that the value of Phi or the Golden Mean is an inherent quality of the Vesica Pisces.

But what does this mean for us?

Some basic facts concerning the Golden Mean.

The ratio of the length of a face of the Great Pyramid (from centre of the bottom of a face to the apex of the pyramid) to the distance from the same point to the exact centre of the pyramid's base square is about 1·6. It is a matter of debate whether this was "intended" to be the golden section number or not.

Euclid (about 300BC) in his "Elements" calls dividing a line at the 0.6180399.. point dividing a line in the extreme and mean ratio. This later gave rise to the name golden mean .

There are no extant records of the Greek architects' plans for their most famous temples and buildings (such as the Parthenon). So we do not know if they deliberately used the golden section in their architectural plans. The American mathematician Mark Barr used the Greek letter phi to represent the golden ratio, using the initial letter of the Greek Phidias who used the golden ratio in his sculptures.